Sólidos Platónicos
Desde la antigüedad de los pueblos neolíticos ya se encuentran registros de los Cuerpos Geométricos conocidos como Sólidos Perfectos, Sólidos Platónicos o Pitagóricos.
Si bien se le adjudica a Pitágoras (569 a.C. – 475 a.C). el descubrimiento, fué Platón (427 a.C – 347 a.C.) quien los describe en su Filosofía.
Para Platón el estudio y conocimiento de estos modelos abstractos son la simbología e ideas primigenias de un orden mayor establecidos en la naturaleza como manifestación de la divinidad.
La belleza de los sólidos regulares no reside en su apariencia física, yace oculta en el ámbito ideal y se basa en su significación filosófica.
La contemplación del mundo es donde estaba la clave para desarrollar la razón y este como modelo hacia el cual hay que elevarse para mejorar y perfeccionar aquel en el cual se desarrolla nuestra vida.
Según la tradición, los sólidos platónicos son representantes del componente divino del mundo y es loable versar sobre “lo que es”, sobre las Formas, las cuales se comunican, están relacionadas entre sí y pueden llegar a ser entendidas no en términos de simetría, sino de analogía y de proporcionalidad.
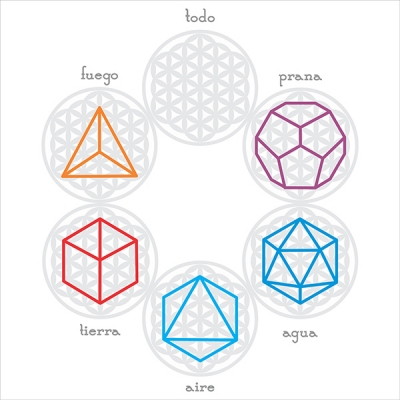
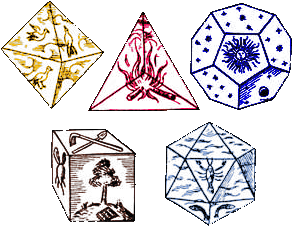
Cada uno de estos cuerpos geométricos representan los elementos de la naturaleza; el Cubo o Hexaedro la Tierra, el Icosaedro el Agua, el Tetraedro el Fuego, el Octaedro el Aire y Dodecaedro el Éter, dentro de una secuencia que va desde la materia más densa hasta el Éter sutil. A partir de un Vacío primigenio y en un proceso que se desenvuelve en forma de espiral a lo largo de ciclos temporales.
Todos estos poliedros regulares convexos coinciden en una particularidad que los hace especiales y los diferencia de otras formas geométricas. Los 5 Sólidos Platónicos son completamente simétricos, tienen todos los lados iguales, todos los ángulos iguales y que los 5 caben dentro de la Matriz Universal que es la Esfera.
Otro requisito que cumplen todos es que si a la cantidad de lados (caras) se le restan la cantidad de aristas (segmento que unen las caras) y se le suman los vértices (ángulos formados por 3 o mas aristas) el resultado siempre es el número 2.
